符号执行例子

程序

注意包含了循环

def f(x, y):
  z = 2 * x
  while z > 0:
    if z == y:
      assert False
    z -= 2

• 限制 x, y 是 BitVec(3), 范围在 [-4, 3].
• 特别注意: \( 2x > 2 \) 是不可能的, 乘法越界时会回绕.
• 显然, 当 \( 2x > 0 \,\land\, y = 2x \), 或 \( 2x-2 > 0 \,\land\, y = 2x-2 \), 或… 的时候会跑到 assert False.
• 导致 assert False 的路径有:
  • \( x=1, y=2 \)
  • \( x=2, y=4 \)
  • \( x=2, y=2 \)
  • \( x=3, y=2 \).

Symbolic Execution Graph

• 你可能以为是

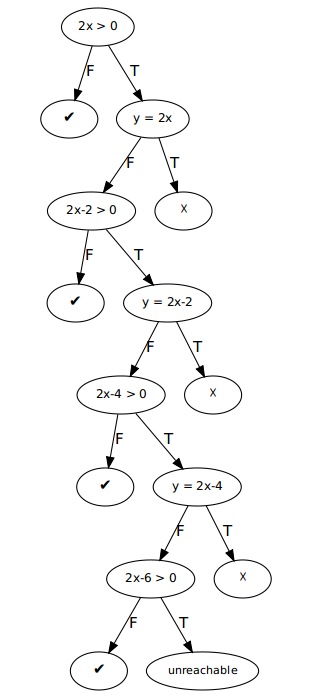
但是其实考虑算术越界后是

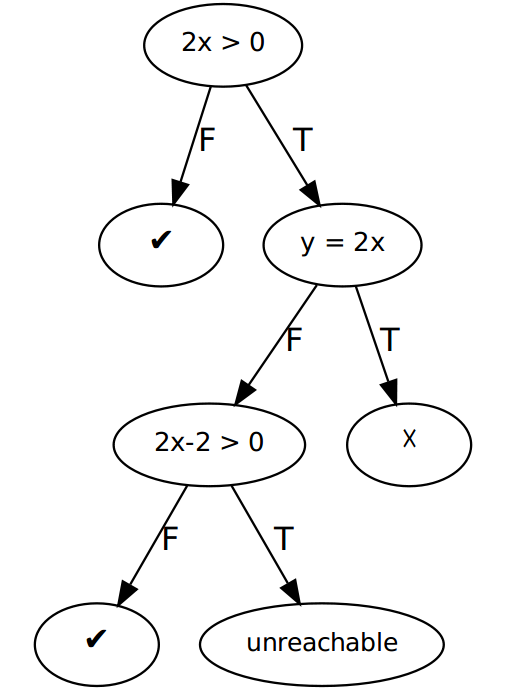
• 基本流程就是探索上面的树, 纯符号执行太简单不说了.

Concolic Execution

1. \( x=0, y=0 \)

• 最初选择输入是 \( x=0, y=0 \), 则探索如图.
• 这时 path condition 是 \( 2x \le 0 \)

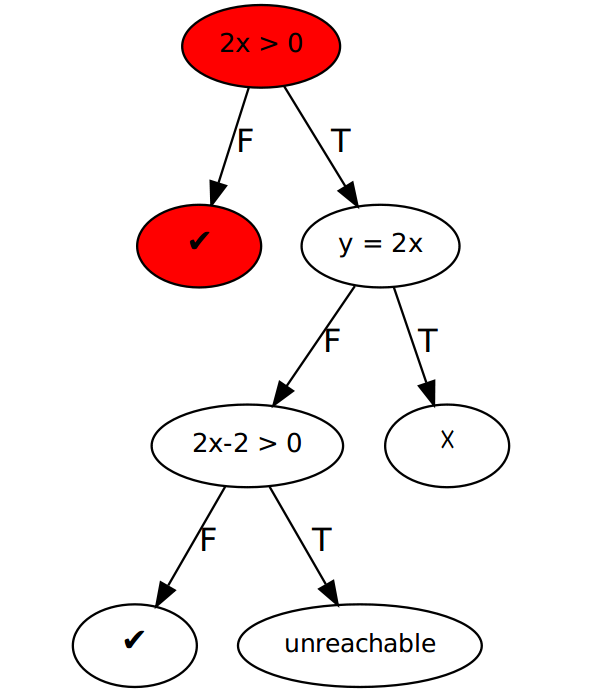
2. \( x=1, y=0 \)

• 希望不要重复 1. 的探索, 所以将其 path condition 取反作为约束 \( \lnot(2x \le 0) \).
• 求解约束, 得到 \( x=1, y=0 \)
• 第二次的探索如图
• 这时 path condition 是 \( 2x > 0 \,\land\, y \neq 2x \,\land\, 2x-2 \le 0 \).

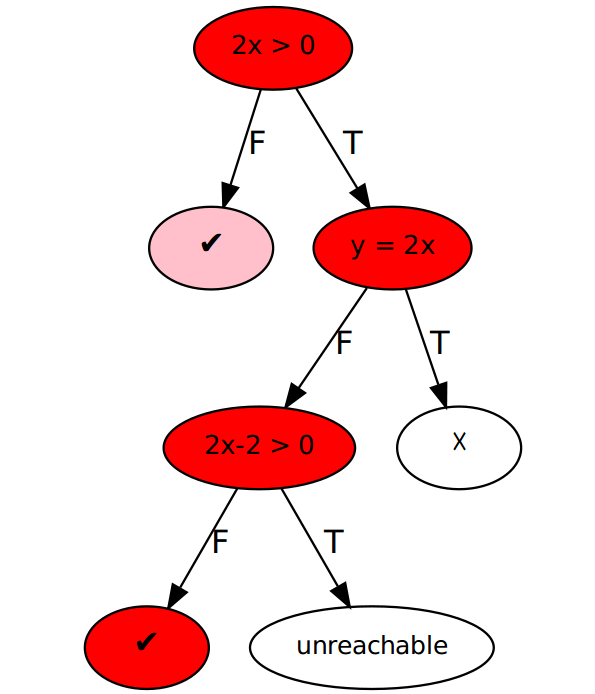
3. \( x=1, y=2 \)

• 不要重复 1. 2. 的探索, 故有约束 \( \lnot(2x \le 0) \) 及 \( \lnot(2x > 0 \,\land\, y \neq 2x \,\land\, 2x-2 \le 0) \).
• 将 2 的 path condition 最后一项取反, 得到约束 \( 2x > 0 \,\land\, y \neq 2x \,\land\, 2x-2 > 0 \).
• 求解约束, 发现不可行: \( 2x-2 \le 0 \) 和 \( 2x-2 > 0 \) 冲突.
• 将 2 的 path condition 最后一项抛去; 倒数第二项取反, 得到约束 \( 2x > 0 \,\land\, y == 2x \)
• 求解约束, 得到 \( x=1, y=2 \)
• 第三次的探索如图

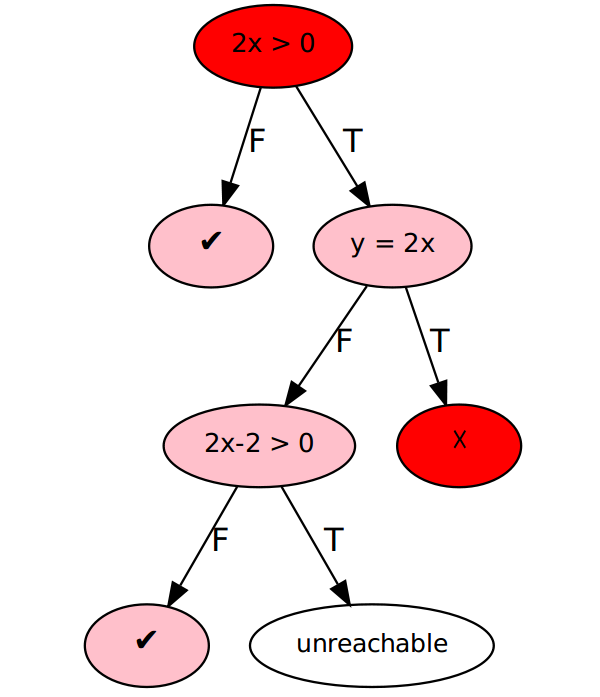
结束

• 继续前面的操作, 加入不重复探索的约束, 然后对前次的 path condition 依次取反.
• 之后的约束都是不可满足的, 故略去.